Capitalisation et actualisation à intérêts simples et à intérêts composes
Intérêts simples – définitions
On dit qu’un capital Co est placé à intérêts simples pour une durée totale de n périodes à un taux d’intérêt i relatif à une période lorsqu’un intérêt périodique It étant calculé pour chaque période en appliquant le taux d’intérêt i sur le capital de départ, on additionne tous ces intérêts périodiques pour obtenir l’intérêt total I. La valeur acquise appelée Cn obtenue après n périodes est calculée en majorant le capital placé Co de l’intérêt total I.
Détermination de l’intérêt :
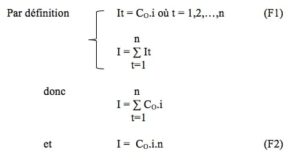
Détermination de la valeur acquise :
Par définition Cn = CO + I
donc Cn = CO + CO .i.n
et Cn = CO (1+ i.n) (F3)
Le facteur de capitalisation IR est le coefficient par lequel le capital actuel connu Co est multiplié pour obtenir la valeur future capitalisée Cn
IR + 1 + i.n
Exemples :
- Déterminez pour un capital de 100.000 euros placé pendant 5 ans à intérêts simples à du 7% l’an :
- a) la rémunération obtenue par le prêteur à la fin de chaque période
- b) l’intérêt total obtenu au bout des 5 ans
- c) la valeur acquise par le capital de départ au bout des 5 ans
Solution :
- a) I = 100.000 . 0,07 = 7 000 soit 7 000 euros reçus au bout de chaque année
- b) I = 100.000 . 0,07.5 = 35 000 soit 35 000 euros d’intérêt reçus au bout des 5 ans c) C5 = 100 000 . (1+0,07.5) = 135 000 euros. Les 100.000 € prêté ont une valeur acquise de 135 000 euros au bout de 5 ans.
- Les mêmes questions sont posées dans le cas d’un capital de un million placé pendant 5 ans à intérêts simples à un taux de 5% par semestre.
Solution :
- It = 100 000 . 0,05 = 5 000 soit 5 000 euros reçus à la fin de chaque semestre
- I = 5 000 . 10 = 50 000 soit 50 000 euros reçus au bout de 10 semestres (5 ans)
- C10 = 100 000 (1+0,05.10) = 150 000 euros. Ce montant correspond à la valeur acquise par les 100.000 € placé à intérêts simples pendant 5 ans au taux de 5% par semestre.
La valeur actuelle Co établie en to équivalente à intérêts simples à un capital Cn, associé au temps tn, soit n périodes plus tard, découle de la formule (F3) si le taux d’actualisation i est relatif à une période.
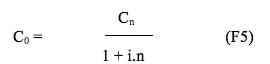
La valeur actuelle Co obtenue par (F5) est encore appelée valeur escomptée par escompte rationnel. Le facteur d’escompte rationnel ER est le coefficient par lequel le capital connu et futur Cn est multiplié pour obtenir la valeur équivalente actualisée Co.
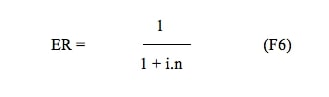
Exemples :
- Quelle est, aujourd’hui, la valeur escomptée par escompte rationnel de 50 000 € à recevoir dans 6 mois si le taux d’intérêt annuel est de 6% ?
Solution : Co = 50 000/(1+0,06.0,5) = 48 543,689 €
Vérification : Co,5 = 48 543,689 . (1+0,06.0,5) = 50 000 €
- Une personne (X) emprunte, à du 8% l’an une somme de 2 000 $, à rembourser dans 9 mois à une autre personne (S). Soit C, le montant à payer par X à S au bout des 9 mois. Trois mois après la date du prêt, S vend la reconnaissance de dette de X à Z, qui désire retirer du 10% de son placement à intérêts simples. Que vaut P3, c’est-à-dire le prix de vente de la reconnaissance de dette?
- Solution :
C9 = 2000(1+0,08.0,75) = 2120$
P3 = 2120 / (1+0,10.0,5) = 2019$
Analyse de la méthode et hypothèses
La méthode de capitalisation à intérêts simples est basée sur deux hypothèses :
Hypothèse 1 (H1): les flux financiers sont certains
On ne met pas en doute le fait que certains paiements seront effectués à certains moments précis dans le temps, que l’emprunteur paiera ses dettes, que l’investissement générera les recettes établies, que l’action procurera un certain dividende, etc.
Dans les enseignements de gestion financière qui font largement appel au principe d’actualisation, cette hypothèse sera évidemment critiquée et différentes solutions seront proposées pour estimer les capitaux futurs de la meilleure façon possible.
Cette hypothèse caractérise en fait les mathématiques financières ou l’algèbre financière.
Les mathématiques viagères, qui découlent des mathématiques financières, sont utilisées dans les compagnies d’assurance car elles font appel aux probabilités liées à l’incertitude de la durée de la vie des individus.
Hypothèse 2 (H2) : le taux d’intérêt est constant et unique
C’est toujours le même taux d’intérêt pour 1 relatif à une période, celui qui a été fixé à la signature du contrat, qui est appliqué pour calculer tous les intérêts périodiques (formule (F1)).
On n’envisage donc pas lors de la capitalisation à intérêts simples que le contrat liant le prêteur à l’emprunteur ait un taux d’intérêt variable, ni que plusieurs taux, connus dès la signature du contrat, puissent être appliqués.
Ces deux hypothèses indiquent que nous travaillons en avenir déterministe, et que les agents économiques ont une connaissance parfaite de tous les flux financiers considérés.
Intérêts composés – Définitions
Les agents économiques en surplus financier qui envisagent de prêter des capitaux vont en général proposer une formule de prêt qui leur procure un intérêt maximum.
Trois stratégies permettent d’obtenir ce maximum, mais l’une d’entre elles, la dernière des trois stratégies qui vont être présentées, celle qui est appelée méthode de capitalisation à intérêts composés, donne l’intérêt de façon immédiate et certaine, alors que les deux autres nécessitent des opérations financières intermédiaires sujettes à des modifications de taux d’intérêt.
1ère stratégie : replacement annuel des intérêts périodiques
Exemple :
Soit 1 000 000 € = le capital Co prêté au temps to
5 ans = la durée du prêt qui s’achève en t5 (n=5)
8% = i le taux d’intérêt annuel
Hypothèses : Les hypothèses 1 et 2 énoncées précédemment sont supposées satisfaites : le prêteur est certain de pouvoir replacer immédiatement les intérêts I4 dès qu’il les perçoit, c’est-à-dire à la fin de chaque période et le taux i est le taux qui sera appliqué à chaque période (hypothèse peu réaliste).
Les intérêts de la période 1 soit I1 ont une valeur de 80 000 € associée au temps t1. Cette somme, replacée pendant 1 an, a une valeur acquise de 86 400 € en t2. A son tour, ce montant peut être replacé pendant un an et devient 93 312 f€ en t3 etc. jusqu’en t5, moment où les 80 000 € du départ sont devenus, par leur replacement à du 8% (hypothèse de taux unique) 108 839 €.
Le même raisonnement peut être suivi pour les 80 000 € qui constituent I2 au temps t2; en t5, ils sont devenus 100 777 €.
De la même manière I3 et I4 deviennent en t5 respectivement 93 313 et 86 400 francs.
Les 80 000 qui constituent I5 ne sont pas replacés, puisqu’ils sont perçus en t5.
En additionnant toutes ces valeurs acquises par les It, on obtient un intérêt total égal à 469 328 francs et les 1 000 000 € prêtés ont acquis en 5 ans une valeur de 1 469 328 €.
Formalisation

Les termes entre crochets sont en progression géométrique de raison (1+i).
Une formule fréquemment utilisée en algèbre financière donne la valeur de la somme de termes en progression géométrique.


2ème stratégie : prêt renouvelé chaque année
Le prêteur ne prête C0 que pour une période. A la fin de celle-ci, il récupère le capital majoré de l’intérêt périodique et reprête l’ensemble pour la période suivante. Il renouvelle l’opération autant de fois qu’il le souhaite.
Les hypothèses 1 et 2 sont supposées satisfaites, or ceci n’est pas évident dans la pratique.
Le même exemple donne les résultats suivants :
- 1 000 000 en t0 deviennent 1 080 000 en t1
- 1 080 000 en t1 deviennent 1 166 400 en t2
- 1 166 400 en t2 deviennent 1 259 712 en t3
- 1 259 712 en t3 deviennent 1 360 489 en t4
- 1 360 489 en t4 deviennent 1 469 328 en t5
Ceci veut dire que selon cette technique, et en supposant que toutes les opérations se sont réalisées au taux de 8% (hypothèse de taux unique), le capital de 1 000 000 € a une valeur acquise de 1 469 328 € en t5, soit le même résultat que la stratégie précédente.
Formalisation

3ème stratégie : capitalisation à intérêts composés
Le prêteur exige que l’emprunteur paie à la fin du prêt, un dédommagement total qui tienne compte des dédommagements It et des intérêts produits par le replacement des I jusqu’à la fin du prêt, à un taux identique à celui appliqué au capital prêté. Les hypothèses 1 et 2 sont encore supposées satisfaites.
Définition de la méthode : Un capital placé pendant n périodes à intérêts composés rapporte un intérêt total calculé en incorporant les intérêts périodiques dans le capital au bout de chaque période de capitalisation. Ces intérêts produisent à leur tour des intérêts jusqu’à la fin de l’opération financière, aux mêmes conditions que le capital de départ.
Formalisation :

Formules :

Conclusions
Ces trois stratégies donnent un résultat rigoureusement équivalent si les hypothèses H1 et H2 sont satisfaites, mais la capitalisation à intérêts composés fixe dès le départ toutes les conditions du prêt, tandis que les deux autres dépendent dans la réalité de l’évolution du taux d’intérêt, et font donc courir au prêteur un risque de taux d’intérêt puisqu’il doit effectuer de nouveaux placements à la fin de chaque période. En conséquence, la méthode de capitalisation à intérêts composés semble la méthode à retenir par le prêteur s’il veut éviter tout risque de taux d’intérêt.
Comparaison des méthodes de capitalisation à intérêts simples (IS) et à intérêts composés (IC)
Première constatation
La formule permettant de trouver avec la méthode des intérêts simples la valeur acquise connaissant la valeur de départ, la durée totale du placement et le taux d’intérêt est une expression linéaire tandis que la formule a une forme exponentielle avec la méthode des intérêts composés.
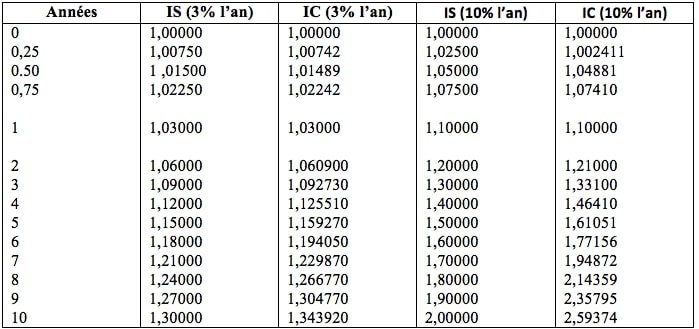
Le tableau 2 met en évidence
- d’une part que l’écart entre les valeurs acquises obtenues à IS et IC est d’autant plus élevé que le taux d’intérêt est élevé et que la durée est longue,
- d’autre part que pour des durées de placement inférieures à la période de capitalisation, la valeur acquise à IS est supérieure à celle obtenue à IC.
Deuxième constatation
Pour |i|<1, ce qui est le cas en pratique, un développement en série de (1+i)n donne :
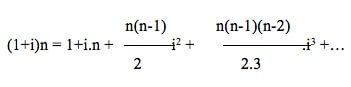
Les deux premiers termes constituent le facteur de capitalisation à intérêts simples IR. Le reste d’ordre 2 est composé de termes d’autant plus négligeables que i et n sont petits. Donc, lorsque le taux d’intérêt est faible et la durée totale du prêt est courte, la valeur acquise à IC est très proche de celle obtenue à IS.
Troisième constatation
La méthode de calcul des intérêts à intérêts simples a comme gros avantage une grande simplicité d’utilisation dans des problèmes financiers élémentaires, mais ne permet pas de résoudre simplement des problèmes financiers dans lesquels on réalise des opérations à des échéances intermédiaires, comme le montre l’exemple ci-dessous :
1° Soit 2 000,-€ placés au taux annuel réel de 8% à intérêts simples pendant 9 mois :
- en le plaçant directement pour 9 mois, on obtient une valeur acquise C9 de 2 120,-€.
- en le plaçant pendant 3 mois, on obtient une valeur acquise C3 de 2 040, €. Si ceux-ci sont replacés pour 6 mois, ils donnent une valeur acquise finale C’9, de 2 121,6 €
- la différence entre C9, et C’9, correspond à l’intérêt pendant 6 mois sur l’intérêt de 40 € obtenu au bout des 3 mois.
2° Si on effectue un escompte rationnel partant de C9, on retrouvera 2000 € mais on n’obtiendra évidemment pas ce résultat en partant de C’9.
3° Si les mêmes opérations de capitalisation sont réalisées à intérêts composés, les valeurs acquises dans les deux cas seront tout à fait identiques et égales à 2 118,84 €. Il n’y aura pas non plus de différences lors de l’opération d’actualisation.


Comments are closed.