Rentabilité et d’un investissement

Hypothèse de taux d’intérêt unique satisfaite

Toute décision d’investir, donc de réaliser une dépense à un certain moment, doit avoir fait l’objet d’une analyse visant à mettre en évidence sa rentabilité : il faut que les recettes futures, compte tenu des dépenses futures et de l’investissement de départ, permettent de générer un bénéfice net suffisant.

Rappelons que l’analyse se fait dans le cadre de ce cours sous les hypothèses de taux unique, d’avenir certain et d’efficacité financière.

Soient :

• D₀        la dépense initiale réalisée en 0
• (R_t,t)    les recettes associées aux temps 1, 2,…, n
• (D_t,t)    les dépenses associées aux temps 1, 2,…, n

Une des méthodes de calcul de la rentabilité d’un investissement consiste à déterminer ce que l’on appelle la valeur actuelle nette (VAN) ou GOODWILL, qui est la valeur actuelle de tous les flux financiers, y compris la dépense initiale, calculée au moment de l’investissement.

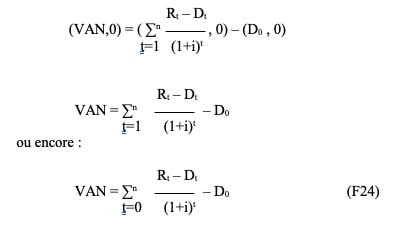
Si la VAN est supérieure à 0, les recettes nettes annuelles (les recettes moins les dépenses) actualisées au moment de l’achat de l’équipement sont supérieures à la dépense initiale, et l’investissement peut être envisagé, mais doit être comparé à d’autres alternatives éventuelles plus rentables.

Si par contre la VAN est inférieure à 0, la dépense initiale ne génère pas de recettes nettes futures suffisantes ; l’investissement doit être rejeté.

Cette présentation de la VAN appelle immédiatement un commentaire très important : la décision d’accepter ou de rejeter un investissement dépend directement du choix du taux d’intérêt utilisé dans les calculs d’actualisation. Le taux d’intérêt que choisissent les financiers pour calculer une VAN correspond en général au « coût d’opportunité du capital », c’est-à-dire au taux de rendement moyen estimé pour un placement également risqué.

En conséquence, pour un investissement donné, plus les recettes sont aléatoires, plus le taux d’actualisation sera élevé. Ceci réduit les recettes nettes actualisées et amène à rejeter plus facilement l’investissement (VAN < 0).

Une autre méthode possible est celle de la recherche d’un taux d’intérêt qui annule la VAN de l’investissement. Ce taux s’appelle le Taux de Rentabilité Interne (TRI).

Les calculettes financières possèdent des programmes donnant une excellente approximation de ce taux, qui ne peut être déterminé de façon exacte. Le chapitre suivant présentera deux méthodes permettant de trouver une approximation du taux d’intérêt recherché.

Ces méthodes permettent de rejeter un investissement si son TRI est insuffisant, ou de choisir l’investissement qui donne le TRI le plus élevé.

Application

Calcul de la VAN pour différents taux d’intérêt et du TRI pour les deux investissements suivants :

Données	Investissement 1	Investissement 2
D0 Rt– Dt t	–  1 000 000 250 000 1, 2,…, 7	– 1 500 000 350 000 1, 2,…, 7

 

i	VAN 1	VAN 2
2,5 5 7,5 10 12,5 15 17,5 20   TRI	587 348 446 593 324 150 217 105 123 075 – 40 105 33 423 – 98 852   16,33 %	722 287 525 231 353 810 203 947 72 305 – 43 853 –  146 792 –  238 393   14,02 %

 

Remarque : outre les 2 méthodes de calcul de la rentabilité d’un investissement présentées, on trouve encore la méthode dite du « Pay Back Period« . Cette méthode, qui détermine le temps nécessaire pour récupérer la dépense initiale grâce aux recettes nettes annuelles, ne repose pas sur l’hypothèse H3 d’efficacité financière et n’est donc pas considérée comme valable dans le cadre de ce cours. Pour les deux investissements présentés ci-dessus, les Pay Back Period sont respectivement de 4 et 4,285 années.

Hypothèse de taux d’intérêt unique non satisfaite

Si on abandonne cette hypothèse, il faut remplacer le taux d’intérêt unique par un taux spécifique à chaque durée séparant la date d’actualisation des moments auxquels les capitaux futurs sont associés.

La formule devient :

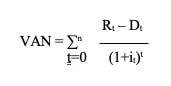
où i_t, est le taux réel correspondant à une immobilisation d’un capital C_t pendant une durée de t périodes.

Cette expression sera utilisée et développée dans d’autres cours à caractère financier.

Détermination de la durée du placement

Formule exacte

Partant de la formule générale de l’intérêt composé F6, il est aisé de trouver la durée du placement nécessaire pour obtenir C_n, partant de C₀ (ou C₀ partant de C_n) si le taux d’intérêt est connu.

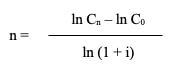
Formule approchée

Il existe une méthode approchée utilisée par les praticiens pour déterminer rapidement le nombre d’années nécessaire pour doubler un capital à intérêts composés, à un taux d’intérêt déterminé :

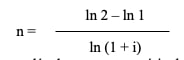
On peut remplacer ln (1 + i) par son développement en série de Mac Laurin limite au deuxième ordre : ln (1 + i) = 0 + i + reste d’ordre 2, donc ln (1 + i) – i

D’autre part, ln 2 = 0,6931… soit approximativement 0,70

Donc   n = 0,70 / i

La formule approchée utilisée en pratique est :

n =   70 /  i (en % l’an)

Exemple : au bout de combien d’années un capital de 1 000 € est-il doublé à intérêts composés si le taux d’intérêt annuel est de 5 % ?

Solution : 14,2067 ans (méthode exacte) et 14 ans (méthode approchée).

Détermination du taux d’intérêt

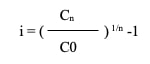
Appliquant la formule générale des intérêts composés F6 et connaissant C_n, C₀ et n. le taux d’intérêt correspondant à cette capitalisation est trouvé par la formule suivante :

Exemple :

• C₀        =          10 000 €
• C_n        =          14 693,3 €
• n          =          5 ans
• i           =          ?

Solution : le taux d’intérêt annuel vaut 0,08 (8%).