Calcul d’annuités avec les mathématiques financières

Que ce soit dans le cadre du remboursement d’un crédit hypothécaire ou de la constitution d’un capital à un terme défini, le calcul des annuités vous permet de définir le montant de paiements réguliers. Explications !

Définition d’une annuité

Une annuité est définie comme une suite de paiements effectués à des échéances équidistantes. Elle est également appelée une « rente ».

De nombreuses opérations financières peuvent être remboursées sous la forme d’une annuité. Par exemple, le crédit hypothécaire contracté pour l’achat d’un immeuble est remboursable par annuité. Des versements mensuels dans un compte d’épargne en vue de se constituer un capital de retraite (ou une rente de retraite), constituent également une (deux) annuité(s). Enfin, les recettes nettes futures annuelles d’un investissement peuvent aussi être considérées comme constituant une annuité.

II existe une terminologie qui permet de décrire rapidement une annuité. En effet, une annuité a des caractéristiques propres relatives

1. aux paiements (constants ou variables)
2. au nombre de paiements (nombre fini ou infini)
3. à la périodicité des paiements (paiements annuels, semestriels,…)
4. au temps qui sépare le premier paiement de la date de la si nature du contrat : les annuités à terme échu ou anticipées, immédiates ou différées correspondent à des définitions précises, mais d’autres situations particulières peuvent se présenter.

On caractérise en général les annuités de la façon suivante :

1. Annuité constante : tous les paiements sont égaux.
2. Annuité variable : les paiements ne sont pas égaux.

Parmi les annuités constantes, on distingue :

• l’annuité unitaire : les paiements valent 1€
• l’annuité quelconque : les paiements sont différents de 1€

Parmi les annuités variables, on distingue :

• l’annuité dont les termes sont en progression arithmétique
• l’annuité dont les termes sont en progression géométrique
• l’annuité variable dont tous les termes sont différents.

Les différentes appellations des annuités

• Annuité a terme échu : chaque paiement relatif à une période est effectué à la fin de cette période.
• Annuité anticipée : chaque paiement relatif à une période est effectué au début de cette période.
• Annuité immédiate : le premier paiement a lieu au cours de la première période qui suit la signature du contrat.
• Annuité différée : un terme constitue d’une ou de plusieurs périodes sépare la signature du contrat de la période au cours de laquelle aura lieu le premier paiement.
• Annuité temporaire : elle comporte un nombre fini de paiements
• Annuité perpétuelle : la suite des paiements équidistants est infinie
• Annuité annuelle : les paiements sont effectués annuellement.
• Annuité fractionnée : les paiements ont lieu à des échéances équidistantes correspondant à des périodes de 1/m^e  d’année

On appelle :

• origine de l’annuité (de la rente) : le moment de la signature du contrat de prêt ou de la dépense initiale dans le cas d’un l’investissement : on l’appellera en général « t₀ » (ou 0 dans un capi-temps).
• le montant de l’emprunt : le capital « E » associe a t₀ qui sera rembourse par une série de paiements constituant une annuité.
• les termes de l’annuité : les différents paiements qui constituent l’annuité : on les appelle en général « a ».
• le nombre de termes est appelé en général « n ». Cependant, pour attirer l’attention sur le fait que l’annuité est fractionnée, on peut exprimer le nombre de termes par n.m, ou n est le nombre d’années et m est le nombre de paiements qui ont lieu dans une année.
• le taux d’intérêt réel utilise dans des opérations d’actualisation ou de capitalisation : il est appelé en général « i » mans peut aussi bien être un taux annuel qu’un taux fractionné. Pour attirer l’attention sur le fait que l’annuité est fractionnée, on peut bien sûr exprimer le taux d’intérêt par i_m ; dans ce cas, le nombre de termes sera n.m.

On appellera enfin :

1. Annuités caractéristiques : les annuités qui sont parfaitement définies a l’aide des définitions énoncées ci-dessus.
2. Annuités particulières : les annuités dont une au moins des propriétés ne correspond pas aux définitions énoncées ci-dessus et les annuités dont les termes sont différents les uns des autres.

Exemples d’annuités caractéristiques

• Une annuité immédiate a terme échu constituée de 5 termes annuels de 1 000 €.
• Une annuité immédiate, anticipée constituée de 5 termes annuels de 1 000 €.
• Une annuité différée de 2 ans, à terme échu, constituée de 5 termes annuels de 1 000 €.
• Une annuité unitaire immédiate trimestrielle perpétuelle à terme échu.
• Une annuité perpétuelle, semestrielle, anticipée, immédiate, croissante selon une progression géométrique de raison 1,08.

Exemples d’annuités particulières

• Une annuité dont les paiements ont lieu tous les 21 jours, immédiate, temporaire, terme échu, quelconque.
• Une annuité annuelle dont le premier paiement a lieu 4 mois après la signature du contrat, à terme échu, temporaire, quelconque, annuelle.
• Une annuité immédiate, à terme échu constituée des termes annuels suivants : 1 000 €, 1 500 €, 780 €, 537 €, 2 180 €.
• Une annuité anticipée, annuelle, temporaire, différé de 2 ans et 3 mois.
• Une annuité constituée par les recettes nettes annuelles d’un investissement associées au milieu de chaque année.

Rôle des annuités en mathématiques financières

On fait appel aux mathématiques financières dans les cas où les hypothèses H1 (avenir certain) et H3 (efficacité financière) sont respectées et où il faut :

1.  trouver un capital, associé à un moment précis dans le temps, qui soit équivalent à une annuité bien déterminée ;
2.  trouver une annuité avec des caractéristiques précises, qui soit équivalente à un capital associé à un moment précis dans le temps.

L’équation des valeurs suffit à résoudre tous les problèmes si on travaille à intérêts composés, même si l’hypothèse de taux d’intérêt unique n’est pas respectée. Rappelons que l’on peut additionner des capitaux s’ils sont ramenés à un même moment. Cependant, le cas 2. ne sera aisément résolu que si l’annuité recherchée est une annuité constante.

Exemples

1-. Trouver le montant E que l’on peut emprunter à du 9% annuel réel aujourd’hui si on s’engage à payer immédiatement annuellement à terme échu l’annuité de 5 termes de 50 000 €.

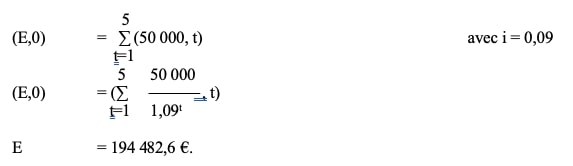
2-. Par quelle annuité immédiate à terme échu constituée de 5 termes annuels peut- rembourser un capital emprunté de 194 482,6 € ?

3-. Vous comptez verser à la fin de chaque mois à partir du mois prochain et ce pendant 10 ans, 10 000 € dans un compte d’épargne qui capitalise les intérêts mensuellement (taux nominal annuel : 12 %). De quel capital C disposerez-vous un mois après le dernier versement ?

La théorie des annuités développée en mathématique financière repose sur les hypothèses H1, H2 (taux d’intérêt unique) et H3. Elle permet de résoudre rapidement un très grand nombre de problèmes financiers quand l’annuité considérée est constante ou croissante suivant une progression géométrique.

Annuité de base

L’annuité de base, à partir de laquelle s’élabore toute la théorie des annuités dans ce cours est l’annuité unitaire, immédiate, temporaire (composée de n termes), à terme échu⁽¹⁾ et annuelle.

Soit      1 €             le terme de l’annuité

n                      le nombre de termes

i                       le taux d’intérêt annuel réel

t₀                      l’origine de la rente

E                      le capital associé à t₀ équivalent à l’annuité définie ci-dessus

Il est fréquent que l’on doive calculer la valeur équivalente à cette annuité à deux moments particuliers : à son origine et au moment du dernier versement.

Valeur équivalente à l’origine de l’annuité

On appelle a_n la somme des valeurs actuelles, calculées à l’origine de l’annuité, des n paiements unitaires qui constituent une annuité unitaire, temporaire, immédiate, à terme échu et annuelle. Soit i le taux d’actualisation.

Par définition, on a :

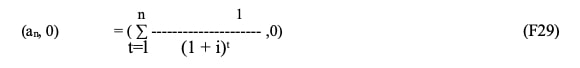
En vertu de l’équation des valeurs, la valeur équivalente à un ensemble de capitaux associés à des temps différents mais ramenés à une même date par actualisation ou capitalisation est obtenue en sommant les résultats obtenus.

(1) dans certains ouvrages, l’annuité de base est l’annuité unitaire, immédiate, temporaire, anticipée et annuelle.

On peut donc écrire :

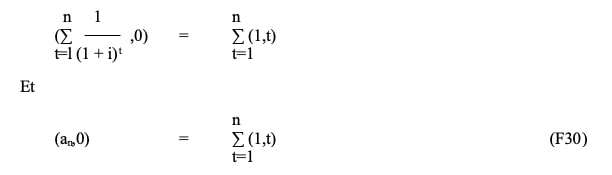
En conséquence, a_n est la valeur équivalente à l’annuité annuelle, unitaire, immédiate, à terme échu, temporaire, associée à l’origine de cette annuité, donc une période avant le premier paiement.

Donc, pour cette annuité de base :

(E,0)    =          (a_n,0)

DÉTERMINATION DE a_n

Multiplier haut et bas par (-1) donne :

Valeur équivalente au moment du dernier versement

On appelle s_n la somme des valeurs acquises, au moment du dernier versement, par les n paiements unitaires qui constituent une annuité unitaire, temporaire, immédiate, à terme échu et annuelle. Soit i le taux utilisé pour les capitalisations.

Par définition, on a :

DÉTERMINATION DE s_n :

Utilisation de tous les ternes de l’annuité

s_n = 1 [ (l+i)^n-1 + (l+i)^n-2 + … + (l+i)^l + (l+i)⁰ ]

s_n = somme de termes en progression géométrique. L’application de la formule F7 donne :

Utilisation de a_n

En vertu de F29 et F33 on peut écrire :

Utilisation de a_n et s_n dans le cas d’annuités caractéristiques

Annuité à terme échu, immédiate, constante, temporaire, quelconque, annuelle

Soient

a          le terme de l’annuité

n          le nombre de termes

i           le taux d’intérêt annuel  réel

t₀          l’origine de la rente

E          le capital associé à to équivalent à l’annuité définie ci-dessus.

Valeur équivalente à l’origine de l’annuité

On appelle A_n la somme des valeurs actuelles, calculées à l’origine de l’annuité des n paiements de a francs qui constituent une annuité à terme échu, immédiate, constante, temporaire, quelconque, annuelle. Soit i le taux d’actualisation.

Par définition, on a :

En conséquence, A_n est la valeur équivalente à l’annuité à terme échu, immédiate, constante, temporaire, quelconque, annuelle, associée à l’origine de cette annuité, donc une période avant le premier versement.

De ce qui précède, on peut encore tirer que : (E,0) = (A_n, 0)

DÉTERMINATION DE A_n

Valeur équivalente au moment du dernier versement

On appelle Sn la somme des valeurs acquises au moment du dernier versement par les n paiements de a € qui constituent une annuité à terme échu, immédiate, constante, temporaire, quelconque, annuelle. Soit i le taux de capitalisation.

Par définition, on a :

En conséquence, Sn est la valeur équivalente à l’annuité à terme échu, immédiate, constante, temporaire, quelconque, annuelle, associée au moment du dernier versement.

DÉTERMINATION DE S_n

1-    Utilisation de tous les ternes de l’annuité

S_n = a (l+i)⁰ + a (l+i)¹ + … + a (l+i)^{n- 1}

S_n = a [(l+i)⁰ + a (l+i)¹ + … + a (l+i)^{n- 1}]

Les termes entre crochets correspondent à s_n, donc

S_n    =  a.s_n                                                                                                                 (F41)

2-    Utilisation de A_n

En vertu de (F37) et (F40), on peut écrire

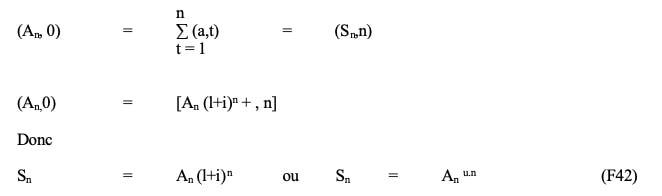
Annuité anticipée, immédiate, constante, temporaire, quelconque, annuelle

Soient

a          le terme de l’annuité

n          le nombre de termes

i           le taux d’intérêt annuel réel

t₀          l’origine de la rente

E          le capital associé à t₀ équivalent à l’annuité définie ci-dessus.

Valeur équivalente l’origine de l’annuité

Ci-dessus, on a mis en évidence le fait que chaque annuité a des caractéristiques propres. Une annuité anticipée et immédiate est telle que le moment de la signature du contrat (t₀) correspond à la date du premier paiement.

1- Premier raisonnement

2- Second raisonnement

L’annuité analysée peut être décomposée en deux parties, telles que :

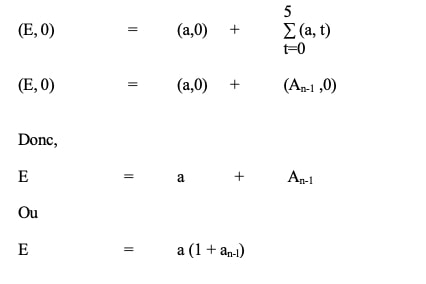
Valeur équivalente au moment du dernier versement

Cette valeur est égale à la somme des valeurs acquises des n paiements de a € qui constituent l’annuité.

Les flux financiers sont tels que l’on retombe immédiatement sur la formule F41.

Valeur équivalente à la fin du prêt

Les versements étant anticipés, la fin du prêt est associée au temps tu, alors que le dernier versement a lieu en t_n-1. On appelle S_n la valeur équivalente à cette annuité en t_n.

Il est clair que S_n = S_n(1+i).

Annuité différée, à terme échu, constante, temporaire, quelconque, annuelle

Soient

a          le terme de l’annuité

n          le nombre de termes

p          le terme différé constitué de p périodes

i           le taux d‘intérêt annuel réel

t₀              l’origine de la rente

E          le capital associé à to équivalent à l’annuité définie ci-dessus.

Valeur équivalente à l’origine de l’annuité

Valeur équivalente à la fin du prêt

Soit V cette valeur.

Il est aisé de montrer que

V = E (1+i)^p+n = A_n (1+i)ⁿ = S_n

Utilisation de a_n ET s_n dans le cas d’annuités particulières

L‘équation des valeurs et les formules F31 et F34 doivent être utilisées à bon escient dans tous les cas pratiques qui n’entrent pas dans les cas classiques vus dans ci-dessus.

L’exemple ci-dessous est développé à titre illustratif.

Quel capital puis-je prêter aujourd’hui si je suis sur(e) de recevoir une annuité payable pendant 15 ans par termes trimestriels de 25 000 €, dont le premier terme est payable

1. a) dans 1 mois
2. b) dans 12 mois

Le taux d’intérêt annuel réel est fixé à 9%.

Résolution :

Détermination du taux d’intérêt et du nombre de termes de l’annuité

Certains problèmes financiers demandent que soit déterminé le taux d’intérêt correspondant à une annuité dont on connaît les caractéristiques suivantes : valeur actuelle (ou valeur acquise), nombre de termes et montant de chacun de ceux-ci.

Cependant, il n’existe pas de méthode analytique permettant de résoudre une équation du n^e degré lorsque n > 3. Même dans le cas où n = 3, la méthode de résolution analytique est difficile et nécessite le recours aux nombres complexes. Il faut donc avoir recours à des méthodes d’estimation.

Estimation de taux d’intérêt par interpolation linéaire

Le tableau ci-dessous montre les valeurs prises par la valeur actuelle et par la valeur acquise d’une annuité temporaire, unitaire, immédiate, à terme échu et annuelle ; les deux graphiques mettent en évidence le caractère non linéaire des résultats.

i	a20	s20
0,14 0,12 0,10 0,08 0,06 0,04 0,02	6,62 7,47 8,51 9,82 11,47 13,59 16,35	91,02 72,05 57,27 45,76 36,79 29,78 24,30

 

Soit

• A_n, la valeur actuelle de l’annuité immédiate, à terme échu, temporaire, quelconque et annuelle
• a le terme de l’annuité
• n le nombre de termes de l’annuité
• i le taux annuel réel recherché

La valeur de a_n peut être déterminée par division de A_n par a. Une fois cette valeur trouvée, la méthode par interpolation exige un travail de tâtonnements pour parvenir à encadrer la vraie valeur a_n par deux autres valeurs actuelles obtenues en prenant des taux d’intérêt voisins de celui que l’on espère obtenir. Ensuite, une « règle de trois » suffira pour obtenir une première estimation du vrai taux d’intérêt. Si ce résultat est trop peu précis, une nouvelle interpolation sera réalisée pour obtenir un résultat plus précis.

MM : On emprunte 281 018 €, qu’il faut rembourser en 20 paiements annuels à terme échu de
25 000 €. Quel est le taux annuel réel appliqué ?

Réponse : a₂₀ = 280 018 : 25 000 = 11,2407

Si i₁= 6%, a₂₀⁽¹⁾ = 11,46992 (interprétation : sii = 6%, la somme des valeurs actuelles des paiements de 1 franc annuellement pendant 20 ans vaut 11,46992 € à l’origine de la rente).

Comme le vrai a₂₀ est inférieur à 11,46992 €, c’est que le vrai taux d’intérêt est supérieur à 6%.

Si i₂ = 6,5%, a₂₀⁽²⁾ = 11,01851 €. De cette manière, on a obtenu deux taux qui encadrent le vrai taux.

Interpolation linéaire :

• une diminution des a₂₀ de 0,45141 € correspond à un accroissement du taux d’intérêt de 0,5%
• une diminution des a₂₀ de 1 € correspond à un accroissement du taux d’intérêt de 0,5%/0,45141
• une diminution des a₂₀ de 0,22922 € correspond à un accroissement du taux d’intérêt de 0,25389%.

La première estimation du taux d’intérêt est de 6% + 0,25389% soit 6,25389%.

Vérification : 25 000 . a₂₀(6,25339%) = 280 930,25 €.

Si une plus grande précision est souhaitée, on effectue une deuxième interpolation linéaire :

Si i = 6,25389%, a₂₀ = 11,23721 €

Le vrai a₂₀ vaut 11,2407 €

Si i = 6,24700% , a₂₀ = 1124343 €

L’interpolation linéaire avec ces données donne la deuxième approximation du taux d’intérêt soit 6,249991%.

Vérification : 25 000 . a₂₀(5,249991%) = 281 020,04 €, soit une erreur de 2 € sur
281 018 €.

Méthode de Newton

La méthode de Newton a pour objectif la découverte des solutions d’une équation du type « f(x) = 0 » où f désigne une fonction d’une variable réelle de classe C¹.

Pour trouver un zéro de f, la méthode procède par approximations successives.

Soit x* une solution (à découvrir) de l’équation f(x) = 0.

Partant d’une valeur approchée x₀ de x*, on en recherche une autre x₁ suivant le procédé illustré ci-dessous :

On détermine la tangente au graphe de f au point (x₀, f(x₀)). Celle-ci a pour équation

y = f(x₀) + (x – x₀).f’(x₀)

La valeur x₁est l’abscisse du point d’intersection de cette tangente avec l’axe des x. Il est donc défini par :

0 = f(x₀) + (x₁ – x₀) . f’(x₀)

d’où

x₁ = x₀ – (f(x₀) /   f’(x₀))

à condition que f’(x₀) soit différent de 0.

Une nouvelle valeur x₂ est obtenue en traçant la tangente au graphe de f au point (x₁, f(x₁)) et en déterminant l’abscisse du point d’intersection de cette tangente avec des x ; on obtient ainsi

x₂ = x₁ – ( f(x₁) /    f’(x₁))

En continuant de la sorte, on définit une suite de valeurs obéissant à la relation de récurrence

x_n+1 = x_n – (  f(x_n) / f’(x_n))

à condition que f’(x_n) ≠ 0 pour toutes les valeurs de n = 0, 1, 2, …

Si la suite x₀,x₁,x₂,… converge, on obtient une solution de l’équation f(x) = 0

N.B. Lorsque la première valeur x0 est bien choisie, la convergence de la suite x₀,x₁,x₂,…peur être extrêmement rapide !

Détermination du nombre de termes de l’annuité

Par définition,  le nombre de termes qui composent une annuité est nécessairement un nombre positif entier, fini dans le cas d’une annuité temporaire, infini dans le cas d’une perpétualité (annuité perpétuelle)^(l).

Problème de base

On emprunte 281 018 €, qu’il faut rembourser par des paiements annuels à terme échu de 25 000 €. i = 6,25 %. Combien de versements seront nécessaires ?

Solution :

25 000 . a_n            =         281 018 €

a_n                      =         11,2407

1 –   (1/ 1,0625n)                 =         11,2407 . 0,0625

On multiplie les deux membres par (-1), et on utilise les logarithmes pour déterminer le nombre de versements à réaliser.

n = 19,99966 soit n = 20 ans.

Problème plus proche de la réalité

L’exemple qui suit illustre les différentes manières équivalentes de résoudre un problème dans lequel la détermination de n donne comme réponse un nombre décimal.

Un emprunt de 200 000 € doit être remboursé en x années par annuités constantes. Les données sont les suivantes : le terme annuel payable à terme échu vaut 42 000 € et le taux d’intérêt annuel réel est égal à 9%.

On demande de déterminer le nombre d’années, obtenu en tronquant la partie décimale du résultat, nécessaire pour rembourser la dette. Le montant complémentaire correspondant à cette partie fractionnaire d’année doit être payé pour équilibrer cette transaction.

Déterminer ce montant complémentaire

• Le cas des annuités perpétuelles sera traité à la fin de ce chapitre.
• S’il est versé au moment du dernier terme de l’annuité
• s’il est versé au moment du premier versement
• s’i1 est versé à une échéance complémentaire

Solution :

n = 6,4937 soit 6 années.

Le montant complémentaire vaut

1)    200000 (109)⁶ – 42 000s₆    =          19 439,95 sort 19 440 € à payer au temps 6

2)    19 439,95 : (1,09)⁵ = 12 634,6 soit 12 635 € à payer au temps 1

3)    à payer au temps 7 : 21 189,5 €.

Annuités perpétuelles

Une annuité perpétuelle ou perpétualité est une série infinie de paiements effectués à des échéances équidistantes. Il est utile de connaître le capital équivalent à cette annuité associé à l’origine de celle-ci.

Annuité perpétuelle, constante, quelconque, immédiate, à terme échu, annuelle

Soit

a         le terme de l’annuité

i           le taux d’intérêt annuel réel

t₀              l’origine de la rente

n = ∞   le nombre de termes est infini

E_p        le capital associé à to équivalent à l‘annuité définie ci-dessus.

Partant de F37 et F38 on peut écrire :

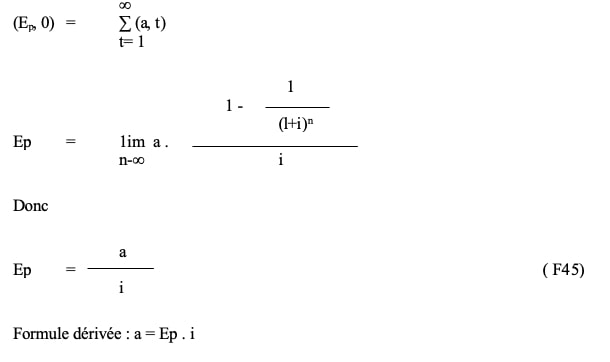
Interprétation : lorsque l’annuité est perpétuelle, l’emprunteur ne paie à échéances équidistantes que l’intérêt sur le capital emprunté, ce qui est logique puisqu’il n’y a pas de remboursement du capital.

Application : dans certains ouvrages traitant de mathématiques financières, on présente l’annuité immédiate, à terme échu, temporaire (n termes), constante, quelconque comme le résultat de la différence entre deux perpétualités, à terme échu, immédiates, constantes, quelconques, l’une débutant en t₀, l’autre en t_n et ayant toutes deux le même terme d’annuité a.

Le capital associé au temps t₀ est la valeur A_n (F38), dont la formule peut être trouvée en soustrayant les valeurs équivalentes aux deux perpétualités, calculées toutes deux en t₀ :

Annuité immédiate, à terme échu, perpétuelle, croissante selon une progression géométrique de raison r < i

Cette annuité est utilisée en gestion financière lorsqu’on veut estimer la valeur des actions d’une société. On suppose que la valeur d’une action est égale à la valeur actuelle de la série infinie des dividendes payés aux actionnaires, en supposant que les dividendes croissent chaque année à un taux de r% (avec r < i, sinon on rencontre des problèmes d‘ordre mathématique).

Soit

a          1e premier terme de l’annuité

(1+r)    la raison

i           le taux d’actualisation annuel réel

t₀          l’origine de la rente

n= ∞    le nombre de tenues infini

Ep        le capital associé à t₀ équivalent à l’annuité définie ci-dessus.

L’annuité est constituée des termes suivants :

a , a(1+r) , a(1+r)² , a(1+r)³ , …

Le capital Ep associé à l’origine de la rente est égal à la somme des valeurs actualisées au temps t₀ de tous les termes de cette annuité :